Kiến thức lũy thừa lớp 12

Trước khi đi vào chi tiết, các thầy cô VUIHOC có nhận định chung về luỹ thừa trong chương trình Toán lớp 12 và mức độ khó của dạng bài tập này trong quá trình ôn thi Toán THPT Quốc gia (dự kiến). Các em cùng theo dõi bảng sau:

Để dễ theo dõi bài viết và dễ trong ôn tập hơn, VUIHOC gửi tặng các em bộ tài liệu ôn tập lý thuyết luỹ thừa lớp 12 đầy đủ và cực kì chi tiết do các thầy cô chuyên môn đặc biệt biên soạn. Nhớ tải về nhé!

>>>Tải xuống file lý thuyết về luỹ thừa lớp 12 bản đầy đủ<<<

1. Ôn lại tổng hợp lý thuyết luỹ thừa lớp 12

1.1. Định nghĩa về luỹ thừa toán 12

Các em có thể hiểu đơn giản theo lý thuyết luỹ thừa rằng, lũy thừa là một phép toán hai ngôi của toán học thực hiện trên hai số a và n, kết quả của phép toán lũy thừa là tích số của phép nhân có n thừa số a nhân với nhau. Ký hiệu:

1.2. Các loại luỹ thừa phổ biến trong chương trình toán 12

Dạng 1: Luỹ thừa với số mũ nguyên

Cho n là một số nguyên dương. Với a là một số thực tuỳ ý, luỹ thừa bậc n của a là tích của n thừa số a. Định nghĩa luỹ thừa với số mũ nguyên cũng giống định nghĩa chung về luỹ thừa. Ta có công thức tổng quát như sau:

an =a.a.a.a…..a (n thừa số a)

Với thì a0 = 1,

Lưu ý:

• 0n và 0-n không có nghĩa

• Luỹ thừa với số mũ nguyên có các tính chất tương tự của luỹ thừa với số mũ nguyên dương.

Dạng 2: Luỹ thừa với số mũ hữu tỉ

Cho số thực a dương và số hữu tỉ 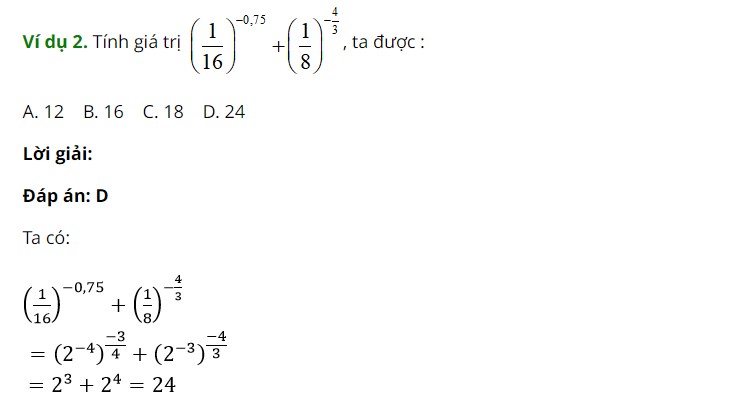, trong đó

Luỹ thừa của số a với số mũ r là số ar xác định bởi:

Đặc biệt: Khi

Dạng 3:

Cho a > 0, , là một số vô tỉ, khi đó với rn là dãy số hữu tỉ thoả mãn

Tính chất của luỹ thừa với số mũ thực:

Cho a, b > 0; x và y ta có các tính chất sau:

ax.ay = ax+y

ax : ay = ax-y

(ax)y = axy

(ab)x = axbx

ax > 0,

ax = ay

Với a > 1 thì ax > ay x > y với 0 < a < 1 thì ax > ay x < y

Với 0 < a < b và m dương thì am < bm; m nguyên âm thì ngược lại am > bm

1.3. Tính chất luỹ thừa

Chúng ta cùng xét các tính chất lũy thừa sau:

• Tính chất về đẳng thức: Cho , ta có:

Tính chất về bất đẳng thức:

• So sánh cùng cơ số: Cho . Khi đó:
  • Với a > 1 thì
  • Với 0 < a < 1 thì

• So sánh cùng số mũ:

  • Với số mũ dương
  • Với số mũ âm

1.4. Tổng hợp các công thức luỹ thừa 12

Về cơ bản, các em cần nắm vững những công thức luỹ thừa lớp 12 căn bản trong bảng sau:

Ngoài ra, luỹ thừa 12 còn có một số công thức khác trong các trường hợp đặc biệt, cụ thể như sau:

• Luỹ thừa của số e:

Số e là hằng số toán học quan trọng, xấp xỉ 2.718 và là cơ số của logarit tự nhiên. Số e được định nghĩa qua giới hạn sau:

Hàm e mũ, được định nghĩa bởi ở đây x được viết như số mũ vì nó thỏa mãn đẳng thức cơ bản của lũy thừa

Hàm e mũ xác định với tất cả các giá trị nguyên, hữu tỷ, thực và cả giá trị phức của x.

Có thể chứng minh ngắn gọn rằng hàm e mũ với x là số nguyên dương k chính là ek

Chứng minh này cũng chứng tỏ rằng ex+y thỏa mãn đẳng thức lũy thừa khi x và y là các số nguyên dương. Kết quả này cũng có thể mở rộng cho tất cả các số không phải là số nguyên dương.

Các em học sinh có thể tham khảo bài viết: Công thức lũy thừa

• Hàm luỹ thừa với số mũ thực:

Lũy thừa với số mũ thực cũng thường được định nghĩa bằng cách sử dụng logarit thay cho sử dụng giới hạn của các số hữu tỷ.

Logarit tự nhiên ln(x) là hàm ngược của hàm mũ ex. Theo đó là số b sao cho x = eb

Nếu a là số thực dương, x là số thực bất kỳ ta có a=eln(a) nên nếu ax được định nghĩa nhờ hàm logarit tự nhiên thì ta cần phải có:

Điều này dẫn tới định nghĩa: ax=ex.lna với mọi số thực x và số thực a

Đăng ký để nhận được bí kíp nắm trọn kiến thức và mọi dạng bài trong bài thi THPT Quốc Gia môn Toán

2. Một số dạng bài tập luỹ thừa lớp 12 thường gặp

Trong vùng kiến thức luỹ thừa 12, có rất nhiều dạng bài tập khác nhau, đa dạng về mức độ có thể khiến các em bối rối trong quá trình giải. Để hệ thống hơn khi ôn tập, VUIHOC đã tổng hợp 3 dạng bài tập luỹ thừa lớp 12 thường gặp nhất trong các đề thi đặc biệt là kì thi THPT Quốc gia.

2.1. Dạng bài tìm điều kiện cơ số của luỹ thừa

Phương pháp giải:

• Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số phải khác 0.
• Khi xét lũy thừa với số mũ không nguyên âm thì cơ số phải dương.

Ta xét ví dụ sau Bài tập 1 trang 60 SGK Giải tích 12

2.2. Dạng bài rút gọn các biểu thức chứa luỹ thừa, căn thức

Để rút gọn các biểu thức đại số chứa luỹ thừa, ta cần linh hoạt sử dụng các hằng đẳng thức đáng nhớ, các tính chất của lũy thừa và tính chất của căn thức.

Ví dụ sau đây sẽ giúp em hiểu rõ hơn về cách làm dạng bài tập luỹ thừa lớp 12:

2.3. Dạng bài so sánh các luỹ thừa

Để so sánh hai lũy thừa ta sử dụng tính chất sau:

Với a, b, m, n N, ta có:

a > b an > bn n

m > n am > an (a > 1)

với a = 0 hoặc a = 1 thì am = an (m.n 0)

Với A,B là các biểu thức, ta có:

An > Bn A > B > 0

Am > An m > n và A > 1

m < n và 0 < A < 1

Phương pháp làm bài: để làm được dạng bài tập này, các em học sinh cần biến đổi 2 lũy thừa thành lũy thừa có cùng cơ số hoặc đưa về có cùng số mũ rồi tiến hành so sánh cơ số. Bên cạnh đó, một phương pháp nâng cao là sử dụng lũy thừa trung gian để so sánh.

3. Bài tập áp dụng các công thức lũy thừa

Để thành thạo bước nhận diện bài toán và áp dụng các công thức luỹ thừa giải bài tập luỹ thừa, các em hãy tải file tổng hợp bài tập luỹ thừa lớp 12 do thầy cô VUIHOC đặc biệt biên soạn dưới đây để ôn luyện hằng ngày nhé!

>>>Tải xuống file bài tập luỹ thừa lớp 12 đầy đủ các dạng kèm giải chi tiết<<<

Đặc biệt, thầy Thành Đức Trung có buổi livestream giải các dạng bài tập luỹ thừa lớp 12 với nhiều mẹo giải hay, giải nhanh và các tip bấm máy tính CASIO vô cùng độc đáo. Các em đừng bỏ qua video bài giảng của thầy Trung dưới đây nhé!

Trên đây là toàn bộ kiến thức về lý thuyết và các dạng bài tập phổ biến về luỹ thừa trong Toán lớp 12. Chúc các em ôn tập tốt và đạt điểm cao!

>>> Bài viết học sinh tham khảo thêm:

Hàm số lũy thừa

Lý thuyết về Logarit

Tập xác định của hàm số lũy thừa

Lũy thừa cùng cơ số

Công thức lũy thừa

Giải nhanh so sánh lũy thừa

Phương pháp giải nhanh bài tập về lũy thừa

Công thức hàm số lũy thừa