
Lý thuyết Phép cộng, phép trừ hai số nguyên Toán 6 Chân trời sáng tạo
Phép cộng, trừ số nguyên
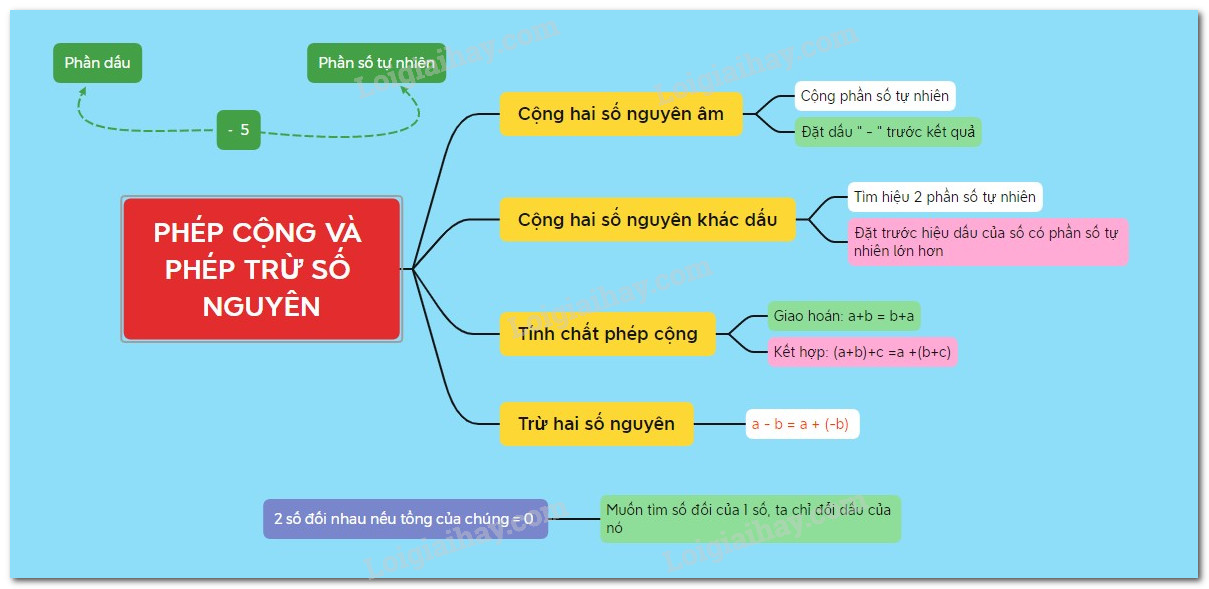
I. Cộng hai số nguyên cùng dấu
1. Phép cộng hai số nguyên dương
Cộng hai số nguyên dương chính là cộng hai số tự nhiên khác (0).
Ví dụ: (2 + 4 = 6).
2. Phép cộng hai số nguyên âm
Để cộng hai số nguyên âm, ta làm như sau:
Bước 1: Bỏ dấu “-” trước mỗi số
Bước 2: Tính tổng của hai số nguyên dương nhận được ở Bước 1.
Bước 3: Thêm dấu “-” trước kết quả nhận được ở Bước 2, ta có tổng cần tìm.
Nhận xét:
- Tổng của hai số nguyên dương là số nguyên dương.
- Tổng của hai số nguyên âm là số nguyên âm.
Chú ý: Cho (a,,,b) là hai số nguyên dương, ta có:
(begin{array}{l}left( { + a} right) + left( { + b} right) = a + bleft( { - a} right) + left( { - b} right) = - left( {a + b} right)end{array})
Ví dụ:
(left( { - 3} right) + left( { - 5} right) = - left( {3 + 5} right) = - 8).
(left( { - 13} right) + left( { - 7} right) = - left( {13 + 7} right) = - 20).
II. Cộng hai số nguyên khác dấu
Nhận xét: Hai số nguyên đối nhau có tổng bằng (0): (a + left( { - a} right) = 0).
Chú ý:
- Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.
- Nếu số dương bằng số đối của số âm thì ta có tổng bằng (0).
- Nếu số dương bé hơn số đối của số âm thì ta có tổng âm.
Ví dụ:
a) (left( { - 8} right) + 2 = - left( {8 - 2} right) = - 6.)
b) (17 + left( { - 5} right) = 17 - 5 = 12).
c) (left( { - 5} right) + 5 = 0) (Do ( - 5) và (5) là hai số đối nhau).
III. Tính chất của phép cộng các số nguyên
Ví dụ 1:
Tính một cách hợp lí: (left( { - 34} right) + left( { - 15} right) + 34)
Ta có:
(left( { - 34} right) + left( { - 15} right) + 34)
(= left( { - 15} right) + left( { - 34} right) + 34) (Tính chất giao hoán)
( = left( { - 15} right) + left[ {left( { - 34} right) + 34} right]) (Tính chất kết hợp)
( = left( { - 16} right) + 0) (cộng với số đối)
( = - 16) (cộng với số 0).
Ví dụ 2:
Trong một ngày, nhiệt độ ở Mát-xcơ-va lúc 5 giờ là ( - {7^o}C), đến 10 giờ tăng thêm ({6^o}C) và lúc 12 giờ tăng thêm ({4^o}C). Nhiệt độ ở Mát-xcơ-va lúc 12 giờ là bao nhiêu?
Giải
Nhiệt độ ở Mát-xcơ-va lúc 12 giờ là:
(left( { - 7} right) + 6 + 4 = left( { - 7} right) + left( {6 + 4} right) = left( { - 7} right) + 10 = 10 - 7 = 3,,left( {^oC} right)).
IV. Phép trừ hai số nguyên
Nhận xét: Phép trừ trong (mathbb{N}) không phải bao giờ cũng thực hiện được, còn phép trừ trong (mathbb{Z}) luôn thực hiện được.
Chú ý: Cho hai số nguyên (a) và (b). Ta gọi (a - b) là hiệu của (a) và (b) ((a) được gọi là số bị trừ, (b) là số trừ).
Ví dụ 1:
a) (6 - 9 = 6 + left( { - 9} right) = - left( {9 - 6} right) = - 3).
b) (8 - left( { - 4} right) = 8 + 4 = 12).
c) ( - 8 - left( { - 9} right) = - 8 + 9 = 9 - 8 = 1).
Ví dụ 2:
Nhiệt độ trong phòng ướp lạnh đang là ({3^o}C), bác Nhung vặn nút điều chỉnh giảm ({4^O}C).Nhiệt độ phòng sau khi giảm là bao nhiêu độ.
Giải
Do bác Nhung giảm nhiệt độ đi ({4^o}C), nên ta làm phép trừ:
(3 - 4 = 3 + left( { - 4} right) = - left( {4 - 3} right) = - 1).
Vậy nhiệt độ phòng ướp lạnh sau khi giảm là ( - {1^o}C).
V. Quy tắc dấu ngoặc
Chú ý:
Trong một biểu thức, ta có thể:
+ Thay đổi tùy ý vị trí của các số hạng kèm theo dấu của chúng.
(a - b - c = - b + a - c = - c - b + a.)
+ Đặt dấu ngoặc để nhóm các số hạng một cách tùy ý. Nếu trước dấu ngoặc là dấu “-” thì phải đổi dấu tất cả các số hạng trong ngoặc.
(a - b - c = left( {a - b} right) - c = a - left( {b + c} right).)
Ví dụ 1:
(begin{array}{l}673 + left[ {2021 - left( {2021 + 673} right)} right] = 673 + left[ {2021 - 2021 - 673} right],,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, = 673 + left( { - 673} right) = 0end{array})
Ví dụ 2:
(begin{array}{l}12 + 13 + 14 - 15 - 16 - 17 = left( {12 - 15} right) + left( {13 - 16} right) + left( {14 - 17} right) = left( { - 3} right) + left( { - 3} right) + left( { - 3} right) = - left( {3 + 3 + 3} right) = - 9end{array}).
Link nội dung: https://blog24hvn.com/cach-cong-tru-so-nguyen-a43428.html