
Bài 30, 31, 32, 33, 34, 35, 36, 37, 38 trang 16, 17 SGK Toán 8 tập 1 - Những hằng đẳng thức đáng nhớ (tiếp) - Luyện tập
Bài 30 trang 16 SGK Toán lớp 8 tập 1
Câu hỏi:
Rút gọn các biểu thức sau:
(,,left( {x + 3} right)({x^2} - 3x + 9) - (54 + {x^3}))
(left( {2x + y} right)(4{x^2} - 2xy + {y^2}) - left( {2x - y} right)(4{x^2} + 2xy + {y^2}))
Phương pháp:
a.
Áp dụng: Hằng đẳng thức tổng hai lập phương, quy tắc phá dấu ngoặc.
({A^3} + {B^3} = left( {A + B} right)({A^2} - AB + {B^2}))
b.
Áp dụng: Hằng đẳng thức tổng hai lập phương, hiệu hai lập phương, quy tắc phá dấu ngoặc.
({A^3} + {B^3} = left( {A + B} right)({A^2} - AB + {B^2}))
({A^3} - {B^3} = left( {A - B} right)({A^2} + AB + {B^2}))
Lời giải:
a) (x + 3)(x2 - 3x + 9) - (54 + x3)
= x3 + 33 - (54 + x3) (Áp dụng HĐT (6) với A = x và B = 3)
= x3 + 27 - 54 - x3
= -27
b) (2x + y)(4x2 - 2xy + y2) - (2x - y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 - 2x.y + y2] - (2x - y)[(2x)2 + 2x.y + y2]
= [(2x)3 + y3] - [(2x)3 - y3]
= (2x)3 + y3 - (2x)3 + y3
= 2y3
Bài 31 trang 16 SGK Toán lớp 8 tập 1
Câu hỏi:
Chứng minh rằng:
a) ({a^3} + {b^3} = {left( {a + b} right)^3} - 3ableft( {a + b} right))
b) ({a^3} - {b^3} = {left( {a - b} right)^3} + 3ableft( {a - b} right))
Áp dụng: Tính ({a^3} + {b^3}) , biết (a . b = 6) và (a + b = -5.)
Phương pháp:
- Biến đổi vế phải của đẳng thức về vế trái đẳng thức.
- Áp dụng các hằng đẳng thức đáng nhớ: lập phương của một tổng hoặc một hiệu, tổng (hiệu) hai lập phương, nhân đơn thức với đa thức.
Lời giải:
a) Biến đổi vế phải ta được:
(a + b)3 - 3ab(a + b)
= a3 + 3a2b + 3ab2 + b3 - 3a2b - 3ab2
= a3 + b3
Vậy a3 + b3 = (a + b)3 - 3ab(a + b)
b) Biến đổi vế phải ta được:
(a - b)3 + 3ab(a - b)
= a3 - 3a2b + 3ab2 - b3 + 3a2b - 3ab2
= a3 - b3
Vậy a3 - b3 = (a - b)3 + 3ab(a - b)
- Áp dụng: Với ab = 6, a + b = -5, ta được:
a3 + b3 = (a + b)3 - 3ab(a + b) = (-5)3 - 3.6.(-5) = -53 + 3.6.5 = -125 + 90 = -35
Bài 32 trang 16 SGK Toán lớp 8 tập 1
Câu hỏi:
Phương pháp:
Áp dụng: Hằng đẳng thức tổng hai lập phương.
({A^3} + {B^3} = left( {A + B} right)({A^2} - AB + {B^2}))
Lời giải:

Bài 33 trang 16 SGK Toán lớp 8 tập 1
Câu hỏi:
a. Tính:
(eqalign{& ,,{left( {2 + xy} right)^2} cr} )
b. (eqalign{& ,,{left( {5 - 3x} right)^2} cr} )
c. (eqalign{& ,,(5 - {x^2})(5 + {x^2}) cr} )
d. (eqalign{& ,,{left( {5x - 1} right)^3} cr} )
e. (eqalign{& ,,left( {2x - y} right)(4{x^2} + 2xy + {y^2}) cr} )
h. (eqalign{& ,,left( {x + 3} right)({x^2} - 3x + 9) cr} )
Phương pháp:
a.
Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.
({left( {A + B} right)^2} = {A^2} + 2AB + {B^2})
b.
Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.
({left( {A - B} right)^2} = {A^2} - 2AB + {B^2})
c.
Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.
({A^2} - {B^2} = left( {A + B} right)left( {A - B} right))
d.
Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.
({left( {A - B} right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3})
e.
Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.
({A^3} - {B^3} = left( {A - B} right)({A^2} + AB + {B^2}))
h.
Áp dụng hằng đẳng thức đáng nhớ để khai triển biểu thức đó.
({A^3} + {B^3} = left( {A + B} right)({A^2} - AB + {B^2}))
Lời giải:
a) (a + b)2 - (a - b)2
= [(a + b) - (a - b)].[(a + b) + (a - b)]
= [a + b - a + b].[a + b + a - b]
= 2b.2a
= 4ab
b) (a + b)3 - (a - b)3 - 2b3
= (a3 + 3a2b + 3ab2 + b3) - (a3 - 3a2b + 3ab2 - b3) - 2b3 (Áp dụng HĐT (4) và (5))
= a3 + 3a2b + 3ab2 + b3 - a3 + 3a2b - 3ab2 + b3 - 2b3
= (a3 - a3) + (3a2b + 3a2b) + (3ab2 - 3ab2) + (b3 + b3 - 2b3)
= 6a2b
c) (x + y + z)2 - 2.(x + y + z).(x + y) + (x + y)2
= [(x + y + z) - (x + y)]2 (Áp dụng HĐT (2) với A = x + y + z ; B = x + y)
= z2.
Bài 35 trang 17 SGK Toán lớp 8 tập 1
Câu hỏi:
a. (eqalign{& ,,{34^2} + {66^2} + 68.66 cr} )
b. (eqalign{& ,,{74^2} + {24^2} - 48.74 cr} )
Phương pháp:
a.
Áp dụng hằng đẳng thức: bình phương của một tổng.
(1),{left( {A + B} right)^2} = {A^2} + 2AB + {B^2})
b.
Áp dụng hằng đẳng thức: bình phương của một hiệu.
(2),{left( {A - B} right)^2} = {A^2} - 2AB + {B^2})
Lời giải:
a) 342 + 68.66 + 662
= 342 + 2.34.66 + 662
= (34 + 66)2
= 1002
= 10 000
b) 742 - 48.74 + 242
= 742 - 2.74.24 + 242
= (74 - 24)2
= 502
= 2 500
Bài 36 trang 17 SGK Toán lớp 8 tập 1
Câu hỏi:
a. (,,{x^2} + 4x + 4) tại (x = 98);
b. (,,{x^3} + 3{x^2} + 3x + 1) tại (x = 99)
Phương pháp:
a. Áp dụng hằng đẳng thức bình phương của một tổng để rút gọn biểu thức, sau đó thay giá trị của (x) để tính giá trị của biểu thức.
({left( {A + B} right)^2} = {A^2} + 2AB + {B^2})
b.
Áp dụng hằng đẳng thức lập phương của một tổng để rút gọn biểu thức, sau đó thay giá trị của (x) để tính giá trị của biểu thức.
({left( {A + B} right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3})
Lời giải:
a) x2 + 4x + 4
= x2 + 2.x.2 + 22
= (x + 2)2
Tại x = 98, giá trị biểu thức bằng (98 + 2)2 = 1002 = 10000
b) x3 + 3x2 + 3x + 1
= x3 + 3.x2.1 + 3.x.12 + 13
= (x + 1)3
Tại x = 99, giá trị biểu thức bằng (99 + 1)3 = 1003 = 1000000
Bài 37 trang 17 SGK Toán lớp 8 tập 1
Câu hỏi:
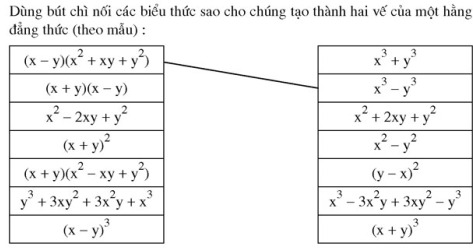
Phương pháp:
Áp dụng các hằng đẳng thức đáng nhớ.
(1),{left( {A + B} right)^2} = {A^2} + 2AB + {B^2})
(2),{left( {A - B} right)^2} = {A^2} - 2AB + {B^2})
(3),{A^2} - {B^2} = left( {A + B} right)left( {A - B} right))
(4),{left( {A + B} right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3})
(5),{left( {A - B} right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3})
(6),{A^3} + {B^3} = left( {A + B} right)({A^2} - AB + {B^2}))
(7),{A^3} - {B^3} = left( {A - B} right)({A^2} + AB + {B^2}))
Lời giải:
Bài 38 trang 17 SGK Toán lớp 8 tập 1
Câu hỏi:
Chứng minh các đẳng thức sau:
a. ({left( {a - b} right)^3} = - {left( {b - a} right)^3});
b. ({left( { - a - b} right)^2} = {left( {a + b} right)^2})
Phương pháp:
a. Áp dụng hằng đẳng thức đáng nhớ: lập phương của một hiệu, sử dụng quy tắc dấu ngoặc, ta biến đổi một vế của đẳng thức thành vế còn lại, ta được điều phải chứng minh.
(5),{left( {A - B} right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3})
b.
Áp dụng hằng đẳng thức đáng nhớ: bình phương của một tổng, sử dụng quy tắc dấu ngoặc, ta biến đổi một vế của đẳng thức thành vế còn lại, ta được điều phải chứng minh.
(1),{left( {A + B} right)^2} = {A^2} + 2AB + {B^2})
Lời giải:
a) Sử dụng tính chất hai số đối nhau:
(a - b)3 = [(-1)(b - a)]3 =(-1)3(b - a)3 = -1.(b - a)3 = -(b - a)3 (đpcm)
b) (-a - b)2 = [(- 1).(a + b)]2 = (-1)2(a + b)2 = 1.(a + b)2 = (a + b)2 (đpcm)
Sachbaitap.com
Link nội dung: https://blog24hvn.com/bai-32-trang-16-sgk-toan-8-tap-1-a49124.html