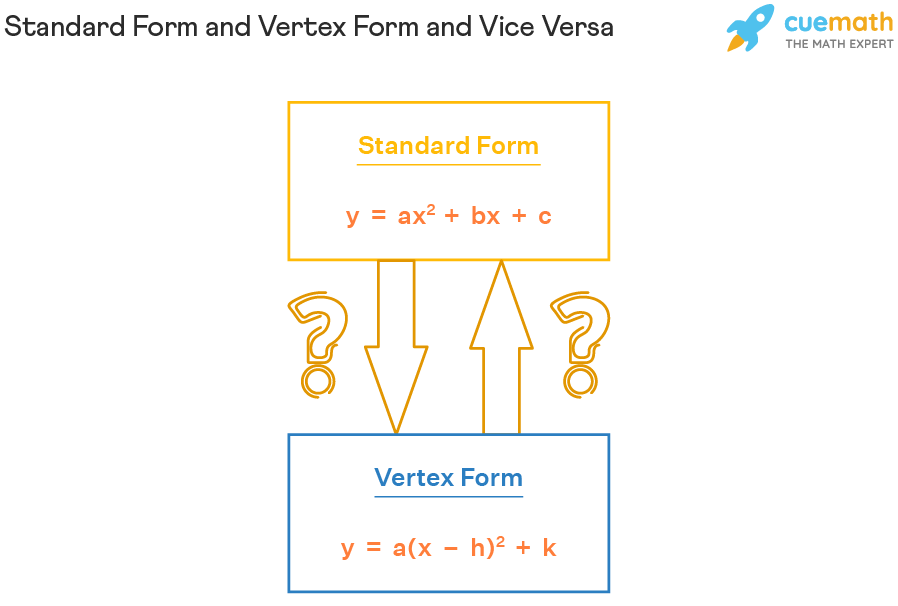
Standard Form to Vertex Form

In this mini-lesson, we will explore the process of converting standard form to vertex form and vice-versa. The standard form of a parabola is y = ax2 + bx + c and the vertex form of a parabola is y = a (x - h)2 + k. Here, the vertex form has a square in it. So to convert the standard to vertex form we need to complete the square.

Let us learn more about converting standard form to vertex form along with more examples.

1. Standard Form and Vertex Form of a Parabola 2. How to Convert Standard Form to Vertex Form? 3. How to Convert Vertex Form to Standard Form? 4. FAQs on Standard Form to Vertex Form

The equation of a parabola can be represented in multiple ways like: standard form, vertex form, and intercept form. One of these forms can always be converted into the other two forms depending on the requirement. In this article, we are going to learn how to convert

• standard form to vertex form and
• vertex form to standard form

Let us first explore what each of these forms means.

Standard Form

The standard form of a parabola is:

• y = ax2 + bx + c

Here, a, b, and c are real numbers (constants) where a ≠ 0. x and y are variables where (x, y) represents a point on the parabola.

Vertex Form

The vertex form of a parabola is:

• y = a (x - h)2 + k

Here, a, h, and k are real numbers, where a ≠ 0. x and y are variables where (x, y) represents a point on the parabola.

In the vertex form, y = a (x - h)2 + k, there is a "whole square". So to convert the standard form to vertex form, we just need to complete the square. But apart from this, we have a formula method also for doing this. Let us look into both methods.

By Completing the Square

Let us take an example of a parabola in standard form: y = -3x2 - 6x - 9 and convert it into the vertex form by completing the square. First, we should make sure that the coefficient of x2 is 1. If the coefficient of x2 is NOT 1, we will place the number outside as a common factor. We will get:

y = −3x2 − 6x − 9 = −3 (x2 + 2x + 3)

Now, the coefficient of x2 is 1. Here are the steps to convert the above expression into the vertex form.

Step 1: Identify the coefficient of x.

Step 2: Make it half and square the resultant number.

Step 3: Add and subtract the above number after the x term in the expression.

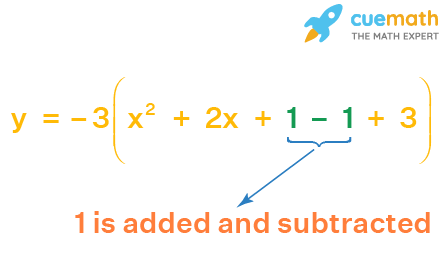
Step 4: Factorize the perfect square trinomial formed by the first 3 terms using the suitable identity.

Here, we can use x2 + 2xy + y2 = (x + y)2.

In this case, x2 + 2x + 1= (x + 1)2

The above expression from Step 3 becomes:

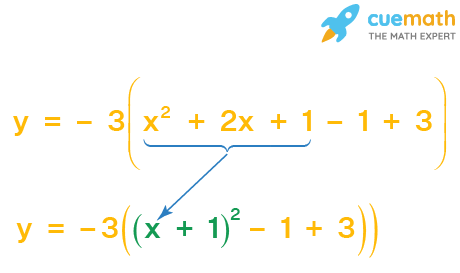
Step 5: Simplify the last two numbers and distribute the outside number.

Here, -1 + 3 = 2. Thus, the above expression becomes:

This is of the form y = a (x - h)2 + k, which is in the vertex form. Here, the vertex is, (h, k)=(-1,-6).

By Using the Formula

In the above method, ultimately we could find the values of h and k which are helpful in converting standard form to vertex form. But the values of h and k can be easily found by using the following steps:

• Find h using h = -b/2a.
• Since (h, k) lies on the given parabola, k = ah2 + bh + c. Just use this to find k by substituting the value of 'h' from the above step.

Let us convert the same example y = -3x2 - 6x - 9 into standard form using this formula method. Comparing this equation with y = ax2 + bx + c, we get a = -3, b = -6, and c = -9. Then

(i) h = -b/2a = -(-6) / (2 × -3) = -1

(ii) k = -3(-1)2 - 6(-1) - 9 = -3 + 6 - 9 = -6

Substitute these two values (along with a = -3) in the vertex form y = a (x - h)2 + k, we get y = -3 (x + 1)2 - 6. Note that we have got the same answer as in the other method.

Which method is easier? Decide and go ahead.

Tips and Tricks:

If the above processes seem difficult, then use the following steps:

• Compare the given equation with the standard form (y = ax2 + bx + c) and get the values of a,b, and c.
• Apply the following formulas to find the values the values of h and k and substitute it in the vertex form (y = a(x - h)2 + k): h = -b/2a k = -D/4a

Here, D is the discriminant where D = b2 - 4ac.

To convert vertex form into standard form, we just need to simplify a (x - h)2 + k algebraically to get into the form ax2 + bx + c. Technically, we need to follow the steps below to convert the vertex form into the standard form.

• Expand the square, (x − h)2.
• Distribute 'a'.
• Combine the like terms.

Example: Let us convert the equation y = -3 (x + 1)2 - 6 from vertex to standard form using the above steps:

y = -3 (x + 1)2 - 6 y = -3 (x + 1)(x + 1) - 6 y = -3 (x2 + 2x + 1) - 6 y = -3x2 - 6x - 3 - 6 y = -3x2 - 6x - 9

Important Notes on Standard Form to Vertex Form:

• In the vertex form, (h, k) represents the vertex of the parabola where the parabola has either maximum/minimum value.
• If a > 0, the parabola has the minimum value at (h, k) and if a < 0, the parabola has the maximum value at (h, k).

☛ Related Topics:

• Vertex Calculator
• Quadratic Function Calculator