Giải Toán 9 bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

VnDoc gửi tới các bạn Giải Toán 9 bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông. Tài liệu tổng hợp câu hỏi và đáp án cho từng câu hỏi trong SGK Toán 9 trang 66, 67, 68, 69, 70, giúp các em học sinh nắm vững kiến thức được học và luyện giải Toán 9 hiệu quả. Sau đây mời các em tham khảo chi tiết.

A. Trả lời câu hỏi trang 66, 67 SGK Toán 9 tập 1

Câu hỏi 1 trang 66 SGK Toán 8 tập 1

Xét hình 1. Chứng minh (Delta AHBsim Delta CHA) . Từ đó suy ra hệ thức (2)

Lời giải chi tiết

Ta có: (widehat{ABH}+widehat{ACH}={{90}^{0}})

Mà (widehat{BAH}+widehat{CAH}={{90}^{0}}Rightarrow widehat{CAH}=widehat{BAH})

Xét tam giác AHB và tam giác CHA có:

(widehat{AHB}=widehat{AHC}={{90}^{0}})

(begin{align} & widehat{CAH}=widehat{BAH} & Rightarrow Delta AHBsim Delta CHA end{align})

Vậy trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên hai cạnh huyền.

Câu hỏi 2 trang 67 SGK Toán 8 tập 1

Xét hình 1. Hãy chứng minh hệ thức (3) bằng tam giác đồng dạng.

Lời giải chi tiết

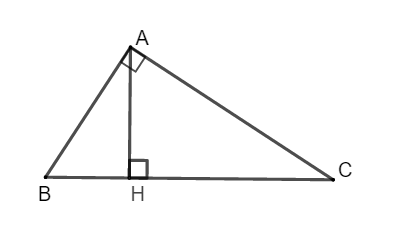
Xét tam giác ABD và tam giác CAB có:

(widehat{B}) chung

(begin{align} & widehat{BAC}=widehat{ADB}={{90}^{0}} & Rightarrow Delta ABDsim Delta CAB & Rightarrow frac{AB}{CA}=frac{AD}{BC} & Rightarrow AB.BC=CA.AD end{align})

Vậy ta có trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.

B. Giải bài tập Toán 9 trang 68, 69 tập 1

Bài 1 (trang 68 SGK Toán 9 Tập 1)

Hãy tính x và y trong mỗi hình sau (hình 4a, b):

Hướng dẫn giải:

a) Đặt tên các đỉnh của tam giác như hình dưới:

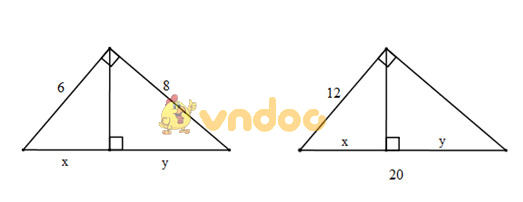
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:

(BC=sqrt{AB^2+AC^2}=sqrt{6^2+8_{_{_{^{^{ }}}}}^2}=10)

Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH

(HC=BC=BH=10-3,6=6,4)

Hay: x = 3,6; y = 6,4

b) Đặt tên các đỉnh của tam giác như hình dưới

Ta vẽ hình và đặt tên thích hợp:

Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH, ta có:

(AB^2=BH.BC=20.xRightarrow x=frac{AB^2}{BC}=frac{12^2}{20}=7,2)

(HC=BC-BH=20-7,2=12,8)

Hayx = 7,2; y = 12,8

Bài 2 (trang 68 SGK Toán 9 Tập 1)

Hãy tính x và y trong hình dưới đây:

Hướng dẫn giải:

Từ đề bài ta có cạnh huyền của tam giác có độ lớn là: 1 + 4 = 5

Áp dụng hệ thức lượng trong tam giác vuông đó là bình phương cạnh góc vuông bằng cạnh huyền nhân hình chiếu của cạnh ấy trên cạnh huyền, ta được:

(x^2=1.5Leftrightarrow x=sqrt{5})(x^2=1.5Leftrightarrow x=sqrt{5})

(y^2=5.4Leftrightarrow y=2sqrt{5})

Bài 3 (trang 69 SGK Toán 9 Tập 1)

Hãy tính x và y trong hình sau:

Hướng dẫn giải:

Xét (Delta{ABC}) vuông tại A. Theo định lí Pytago, ta có:

(BC^2=AB^2+AC^2)

(Leftrightarrow y^2=5^2+7^2 Leftrightarrow y^2=25+49)

(Leftrightarrow y^2=74 Leftrightarrow y=sqrt{74})

Áp dụng hệ thức liên quan đến đường cao trong tam giác vuông, ta có:

(dfrac{1}{AH^2}=dfrac{1}{AB^2}+dfrac{1}{AC^2})

(Leftrightarrow dfrac{1}{x^2}=dfrac{1}{5^2}+dfrac{1}{7^2} Leftrightarrow dfrac{1}{x^2}=dfrac{1}{25}+dfrac{1}{49})

(Leftrightarrow dfrac{1}{x^2}=dfrac{49}{25.49}+dfrac{25}{25.49} Leftrightarrow dfrac{1}{x^2}=dfrac{49+25}{25.49})

(Leftrightarrow dfrac{1}{x^2}=dfrac{74}{1225} Leftrightarrow x=sqrt{dfrac{1225}{74}})

(Leftrightarrow x=dfrac{35sqrt{74}}{74})

Vậy ( x=dfrac{35sqrt{74}}{74}, , y=sqrt {74})

Bài 4 (trang 69 SGK Toán 9 Tập 1)

Hãy tính x và y trong hình sau:

Hướng dẫn giải:

Đặt tên các đỉnh của tam giác như hình bên dưới

Áp dụng hện thức h2 = b'c' ta có:

(AH^2=HB.HCRightarrow=frac{AH^2}{HB}=4)

(AC^2=BC.HCRightarrow y^2=5.4=20Rightarrow y=sqrt{20}=2sqrt{5})

Nhận xét: Ta có thể tính y theo định lý Pi-ta-go:

(y^2=2^2+4^2=20Rightarrow y=sqrt{20}=2sqrt{5})

C. Giải bài tập Toán 9 trang 69, 70 phần Luyện tập

Bài 5 (trang 69 SGK Toán 9 Tập 1)

Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.

Hướng dẫn giải:

Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:

(BC=sqrt{AB^2+AC^2}=sqrt{3^2+4^2}=5)

Áp dụng hệ thức lượng vào các tam giác ABC vuông tại A, AHB vuông tại H, AHC vuông tại H, ta có:

(AH.BC=AB.ACRightarrow AH=frac{AB.AC}{BC}=frac{3.4}{5}=2,4)

(AB^2=BC.BHRightarrow BH=frac{AB^2}{BC}=frac{3^2}{5}=1,8)

CH = BC - BH = 5 - 1,8 = 3,2

Bài 6 (trang 69 SGK Toán 9 Tập 1)

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.

Giải:

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH, ta có:

(AH^2=BH.CHRightarrow AH=sqrt{BH.CH}=sqrt{1.2}=sqrt{2})

Áp dụng định lí Pytago vào tam giác ABH vuông tại H, ta có:

(AH=sqrt{BH^2+AH^2}=sqrt{1+2}=sqrt{3})

Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:

(AC=sqrt{BC^2-AB^2}=sqrt{3^2-3}=sqrt{6})

Bài 7 (trang 69 SGK Toán 9 Tập 1)

Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x2=ab ) như trong hai hình sau:

Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

Hướng dẫn giải:

Cách 1: Đặt tên các đoạn thẳng như hình bên.

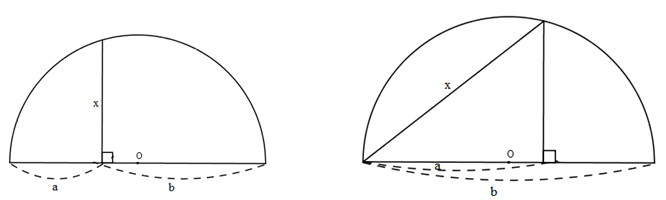
Xét tam giác ABC ta có:

(OA=OB=OC=frac{BC}{2}left(=Rright))

Suy ra ∆ABC vuông tại A.

Áp dụng hệ thức h2 = b'c' ⇒ x2 = ab

Cách 2: Vẽ và đặt tên như hình bên dưới

Xét tam giác ABC ta có:

(OA=OB=OC=frac{BC}{2}left(=Rright))

Suy ra ∆ABC vuông tại A.

Áp dụng hệ thức AB2=BC.BH⇒x2=ab

Bài 8 (trang 70 SGK Toán 9 Tập 1)

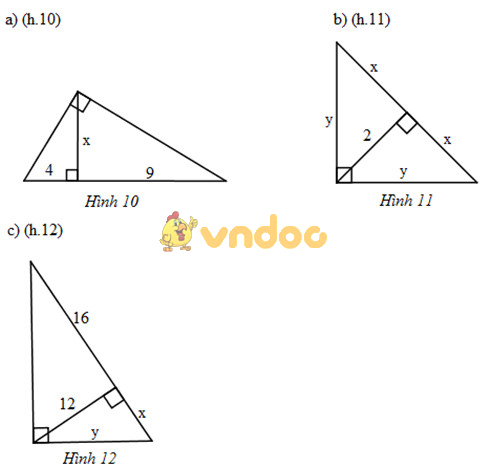
Tìm x và y trong mỗi hình sau:

Hướng dẫn giải:

a) Dùng hệ thức lượng bình phương đường cao bằng tích hai hình chiếu hai cạnh góc vuông lên cạnh huyền h2=b′c′

⇒ x2 =4.9 = 36 ⇒ x = 6

b) Xét tam giác ABC có cạnh huyền là 2x, ta nhận thấy rằng, tam giác này là tam giác vuông cân. Mặc khác, đường cao của tam giác này có độ lớn bằng 2 nên:

(2x=sqrt{y^2+y^2}=sqrt{8+8}=4Rightarrow x=2)

c) Xét tam giác vuông lớn, ta có:

122 = 16x ⇒ x = 9

Xét tam giác vuông có cạnh huyền là y, ta có:

(y^2=sqrt{12^2+9^2}=15)

Bài 9 (trang 70 SGK Toán 9 Tập 1)

Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và Tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông goác với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng

a) Tam giác DIL là một tam giác cân;

b) Tổng (frac{1}{DI^2}+frac{1}{DK^2}) không đổi khi I thay đổi trên cạnh AB.

Hướng dẫn giải:

a) Xét (Delta ADI và Delta CDL) có:

(widehat{A}=widehat{C}= 90^{circ})

AD=CD (hai cạnh hình vuông)

(widehat{D_{1}}=widehat{D_{2}} (cùng phụ với widehat{CDI}))

Do đó (Delta ADI=Delta CDL) (g.c.g)

Suy ra DI=DL.

Vậy (Delta DIL) cân (đpcm).

b) Xét (Delta{DLK}) vuông tại D, đường cao DC.

Áp dụng hệ thức (dfrac{1}{h^{2}}=dfrac{1}{b^{2}}+dfrac{1}{c^{2}}), ta có:

(dfrac{1}{DC^{2}}=dfrac{1}{DL^{2}}+dfrac{1}{DK^{2}}) (mà DL=DI)

Suy ra (dfrac{1}{DC^{2}}=dfrac{1}{DI^{2}}+dfrac{1}{DK^{2}})

Do DC không đổi nên (dfrac{1}{DI^{2}}+dfrac{1}{DK^{2}})là không đổi.

Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức (dfrac{1}{h^{2}}=dfrac{1}{b^{2}}+dfrac{1}{c^{2}})

Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.

...............................

Bài tiếp theo: Giải Toán 9 bài 2: Tỉ số lượng giác của góc nhọn

Xem thêm:

• Toán 9 Bài 1
• Một số hệ thức về cạnh và đường cao trong tam giác vuông

Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải bài tập Toán 9 bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông. Hy vọng thông qua tài liệu này, các em học sinh sẽ biết cách giải các bài tập trong SGK Toán lớp 9, từ đó nâng cao kỹ năng giải Toán 9 và học tốt Toán 9 hơn. Để xem lời giải những bài tiếp theo, mời các bạn vào chuyên mục Soạn Toán 9 trên VnDoc nhé.

Ngoài tài liệu trên, mời các bạn tham khảo thêm Toán lớp 9, Giải bài tập Toán lớp 9, Tài liệu học tập lớp 9, và các đề học kì 1 lớp 9; đề thi học kì 2 lớp 9 được cập nhật liên tục trên VnDoc.