100 bài tập Giới hạn của hàm số (có đáp án 2024) và cách giải

Giới hạn của hàm số và cách giải bài tập - Toán lớp 11

1. Lý thuyết về giới hạn của hàm số

a) Giới hạn của hàm số tại một điểm

* Giới hạn hữu hạn: Cho khoảng K chứa điểm x0 . Ta nói rằng hàm số f(x) xác định trên K (có thể trừ điểm x0) có giới hạn là L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn∈Kx0 và xn→x0, ta có: f(xn)→L

Kí hiệu:limx→x0f(x)=L hay f(x)→L khi x→x0.

Nhận xét: Nếu f(x) là hàm số sơ cấp xác định tại x0 thì limx→x0fx=fx0.

* Giới hạn ra vô cực:

Hàm số y = f(x) có giới hạn dần tới dương vô cực khi x dần tới x0 nếu với mọi dãy số (xn):xn→x0 thì f(xn)→+∞.

Kí hiệu: .

Hàm số y = f(x) có giới hạn dần tới âm vô cực khi x dần tới x0 nếu với mọi dãy số (xn):xn→x0 thì f(xn)→−∞.

Kí hiệu: limx→x0f(x)=−∞.

b) Giới hạn của hàm số tại vô cực

* Giới hạn ra hữu hạn:

- Ta nói hàm số y = f(x) xác định trên (a;+∞) có giới hạn là L khi x→+∞ nếu với mọi dãy số (xn):xn>a và xn→+∞ thì f(xn)→L.

Kí hiệu: limx→+∞f(x)=L.

- Ta nói hàm số y = f(x) xác định trên (−∞;b) có giới hạn là L khi x→−∞ nếu với mọi dãy số (xn):xn<b và xn→−∞ thì f(xn)→L.

Kí hiệu: limx→−∞f(x)=L.

* Giới hạn ra vô cực:

- Ta nói hàm số y = f(x) xác định trên (a;+∞) có giới hạn dần tới dương vô cùng (hoặc âm vô cùng) khi x→+∞ nếu với mọi dãy số (xn):xn>a và xn→+∞ thì f(xn)→+∞ (hoặc f(xn)→−∞).

Kí hiệu: limx→+∞f(x)=+∞ (hoặc limx→+∞f(x)=-∞).

- Ta nói hàm số y = f(x) xác định trên (−∞;b) có giới hạn là dần tới dương vô cùng (hoặc âm vô cùng) khi x→−∞ nếu với mọi dãy số (xn):xn<b và xn→−∞ thì f(xn)→+∞. (hoặc f(xn)→−∞).

Kí hiệu: limx→-∞f(x)=+∞ (hoặc limx→-∞f(x)=−∞).

c) Các giới hạn đặc biệt

d) Một vài định lý về giới hạn hữu hạn

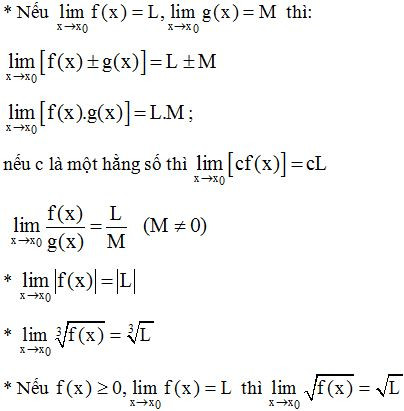
Chú ý:

- Các định lý về giới hạn hữu hạn của hàm số vẫn đúng khi thay x→x0 bởi x→+∞ hoặc x→-∞.

- Định lí trên ta chỉ áp dụng cho những hàm số có giới hạn là hữu hạn. Ta không áp dụng cho các giới hạn dần về vô cực.

* Nguyên lí kẹp:

Cho ba hàm số f(x), g(x), h(x) xác định trên K chứa điểm x0 (có thể các hàm đó không xác định tại x0). Nếu g(x)≤f(x)≤h(x) ∀x∈Klimx→x0g(x)=limx→x0h(x)=L thì .

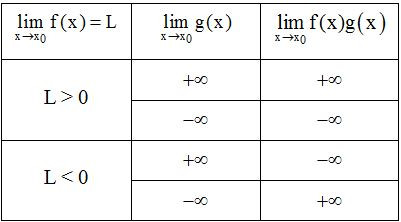
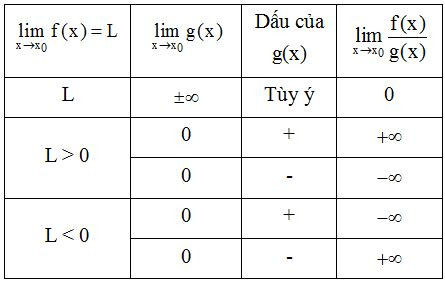
e) Quy tắc về giới hạn vô cực

Quy tắc tìm giới hạn của tích f(x)g(x)

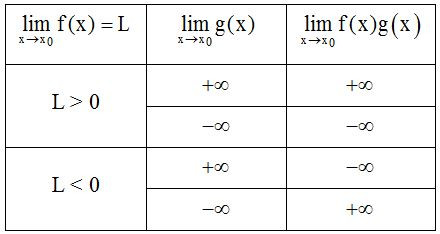
Quy tắc tìm giới hạn của thương f(x)g(x)

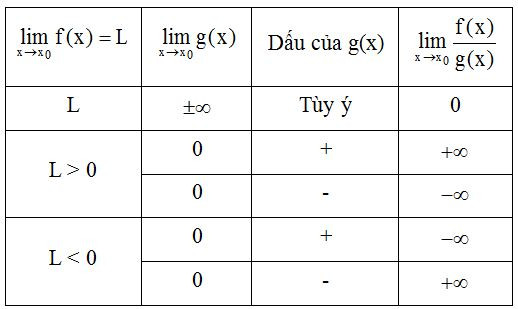
f) Giới hạn một bên

* Giới hạn hữu hạn:

- Định nghĩa 1: Giả sử hàm số f xác định trên khoảng x0;b,x0∈ℝ. Ta nói rằng hàm số f có giới hạn bên phải là số thực L khi dần đến x0 (hoặc tại điểm x0) nếu với mọi dãy số bất kì (xn) những số thuộc khoảng (x0; b) mà lim xn = x0 ta đều có lim f(xn) = L.

Khi đó ta viết: limx→x0+fx=L hoặc fx→L khi x→x0+.

- Định nghĩa 2: Giả sử hàm số f xác định trên khoảng a;x0,x0∈ℝ. Ta nói rằng hàm số có giới hạn bên trái là số thực L khi x dần đến x0 (hoặc tại điểm x0) nếu với mọi dãy bất kì (xn) những số thuộc khoảng (a; x0) mà lim xn = x0 ta đều có lim f(xn) = L.

Khi đó ta viết: limx→x0−fx=L hoặc fx→L khi x→x0−.

- Nhận xét:

limx→x0fx=L⇔limx→x0−fx=limx→x0+fx=L

Các định lí về giới hạn của hàm số vẫn đúng khi thay x→x0 bởi x→x0− hoặc x→x0+.

* Giới hạn vô cực:

- Các định nghĩa limx→x0−fx=+∞, limx→x0−fx=−∞, limx→x0+fx=+∞ và limx→x0+fx=−∞ được phát biểu tương tự như định nghĩa 1 và định nghĩa 2.

- Nhận xét: Các định lí về giới hạn của hàm số vẫn đúng nếu thay L bởi +∞ hoặc -∞

2. Các dạng bài tập

Dạng 1: Giới hạn tại một điểm

Phương pháp giải:

- Nếu f(x) là hàm số sơ cấp xác định tại x0 thì limx→x0fx=fx0

- Áp dụng quy tắc về giới hạn tới vô cực:

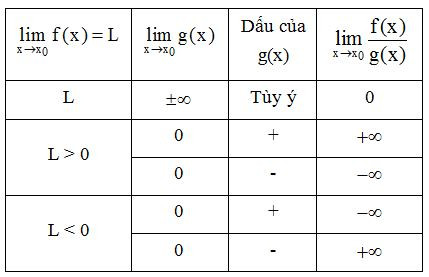
Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

Lời giải

Ví dụ 2: Tính các giới hạn sau:

Lời giải

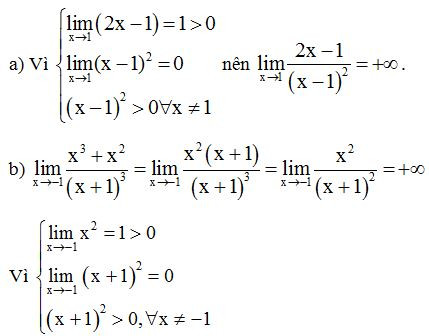
Dạng 2: Giới hạn tại vô cực

Phương pháp giải:

- Rút lũy thừa có số mũ lớn nhất

- Áp dụng quy tắc giới hạn tới vô cực

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) limx→+∞(7x5+5x2−x+7)

b) limx→−∞4x5−3x3+x+1

Lời giải

Ví dụ 2: Tính các giới hạn sau:

a) limx→+∞x6+5x−1

b) limx→−∞2x2+1+x

Lời giải

Dạng 3: Sử dụng nguyên lý kẹp

Nguyên lí kẹp:

Cho ba hàm số f(x), g(x), h(x) xác định trên K chứa điểm x0 (có thể các hàm đó không xác định tại x0). Nếu g(x)≤f(x)≤h(x) ∀x∈Klimx→x0g(x)=limx→x0h(x)=L thì limx→x0f(x)=L.

Phương pháp giải:

Xét tính bị chặn của hàm số f(x) bởi hai hàm số g(x) và h(x) sao cho limx→x0g(x)=limx→x0h(x)=L

Chú ý tính bị chặn của hàm số lượng giác:

−1≤sinx≤1−1≤cosx≤1

Ví dụ minh họa:

Ví dụ 1: Tính giới hạn của hàm số:

a) limx→0x2cos2nx

b) limx→−∞cos5x2x

Lời giải

Ví dụ 2: Tính giới hạn của hàm số: limx→+∞2sinx+cos3xx+1−x

Lời giải

Dạng 4: Giới hạn dạng vô định 00

Nhận biết dạng vô định 00: Tính limx→x0f(x)g(x) trong đó f(x0) = g(x0) = 0.

Phương pháp giải:

Để khử dạng vô định này ta phân tích f(x) và g(x) sao cho xuất hiện nhân tử chung là (x - x0)

Định lí: Nếu đa thức f(x) có nghiệm x = x0 thì ta có: f(x) = (x - x0)f1(x).

* Nếu f(x) và g(x) là các đa thức thì ta phân tích f(x) = (x - x0)f1(x) và g(x) = (x - x0)g1(x).

Khi đó limx→x0f(x)g(x)=limx→x0f1(x)g1(x), nếu giới hạn này có dạng 00 thì ta tiếp tục quá trình như trên.

Chú ý: Nếu tam thức bậc hai ax2 + bx + c có hai nghiệm x1 ; x2 thì ta luôn có sự phân tích: ax2 + bx + c = a(x - x1) (x - x2)

* Nếu f(x) và g(x) là các hàm chứa căn thức thì ta nhân lượng liên hợp để chuyển về các đa thức, rồi phân tích các đa thức như trên.

Các lượng liên hợp:

* Nếu f(x) và g(x) là các hàm chứa căn thức không đồng bậc ta sử dụng phương pháp tách, chẳng hạn:

Nếu u(x)n,v(x)m→c thì ta phân tích:

u(x)n−v(x)m=(u(x)n−c)−(v(x)m−c)

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

a) limx→1x3−3x2+2x2−4x+3

b) limx→22x2−5x+2x3−8

Lời giải

a) limx→1x3−3x2+2x2−4x+3

=limx→1(x−1)(x2−2x−2)(x−1)(x−3)=limx→1x2−2x−2x−3=32

b) limx→22x2−5x+2x3−8

=limx→2(2x−1)(x−2)(x−2)(x2+2x+4)=limx→22x−1x2+2x+4=14

Ví dụ 2: Tính các giới hạn sau:

Lời giải

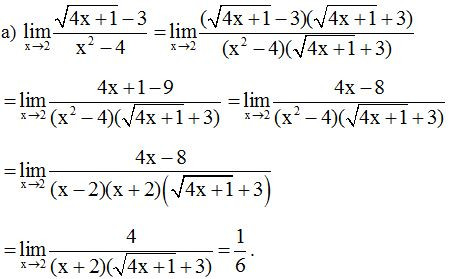
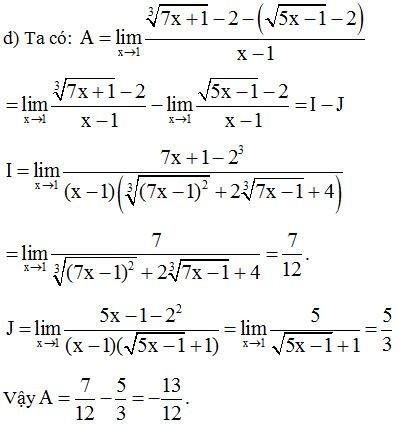
Dạng 5: Giới hạn dạng vô định ∞∞

Nhận biết dạng vô định ∞∞

limx→x0uxvx khi limx→x0ux=±∞,limx→x0vx=±∞

limx→±∞uxvx khi limx→x0ux=±∞,limx→x0vx=±∞

Phương pháp giải:

- Chia tử và mẫu cho xn với n là số mũ cao nhất của biến ở mẫu (Hoặc phân tích thành tích chứa nhân tử xn rồi giản ước).

- Nếu u(x) hoặc v(x) có chứa biến x trong dấu căn thì đưa xk ra ngoài dấu căn (Với k là mũ cao nhất của biến x trong dấu căn), sau đó chia tử và mẫu cho lũy thừa cao nhất của x.

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

Lời giải

Ví dụ 2: Tính các giới hạn sau:

Lời giải

Dạng 6: Giới hạn dạng vô định ∞−∞ và 0.∞

Phương pháp giải:

- Nếu biểu thức chứa biến số dưới dấu căn thì nhân và chia với biểu thức liên hợp

- Nếu biểu thức chứa nhiều phân thức thì quy đồng mẫu và đưa về cùng một biểu thức

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

Lời giải

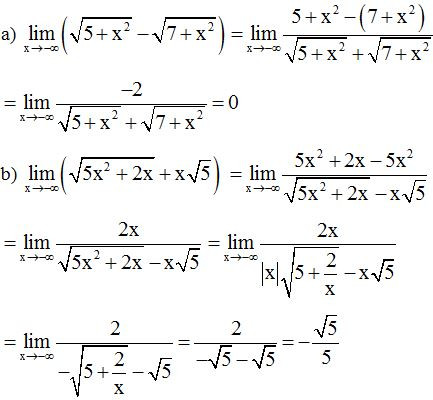
Ví dụ 2: Tính các giới hạn sau:

a) limx→01x−1x2

b) limx→01x1x+1−1

Lời giải

Dạng 7: Tính giới hạn một bên

Phương pháp giải:

Sử dụng quy tắc tính giới hạn tới vô cực

Ví dụ minh họa:

Ví dụ 1: Tính các giới hạn sau:

Lời giải

Ví dụ 2: Cho hàm số fx=x2+11−x khi x<12x−2 khi x≥1. Tính:

a) limx→1+fx

b) limx→1−fx

Lời giải

a) limx→1+fx=limx→1+2x−2=2.1−2=0

b) limx→1−fx=limx→1−x2+11−x=+∞ vì limx→1−x2+1=2>0limx→1−1−x=0x→1−⇒x<1⇒1−x>0

Dạng 8: Tìm tham số m để hàm số có giới hạn tại 1 điểm cho trước

Phương pháp giải:

Sử dụng nhận xét: limx→x0fx=L⇔limx→x0−fx=limx→x0+fx=L

- Tính giới hạn limx→x0−fx;  limx→x0+fx

- Để hàm số có giới hạn tại x = x0 cho trước thì limx→x0−fx= limx→x0+fx. Tìm m.

Khi đó với m vừa tìm được, hàm số có giới hạn tại x = x0 cho trước và giới hạn đó bằng L=limx→x0−fx= limx→x0+fx

Ví dụ minh họa:

Ví dụ 1: Cho hàm số fx=x2−3x+2x−2 x>2a x≤2. Với giá trị nào của a thì hàm số đã cho có giới hạn tại điểm x = 2?

Lời giải

Ta có

limx→2+fx=limx→2+x2−3x+2x−2=limx→2+x−1x−2x−2=limx→2+x−1=1

limx→2−fx=a.

Để hàm số có giới hạn tại x = 2 thì limx→2+fx= limx→2−fx.

⇒a=1

Vậy a = 1.

Ví dụ 2: Tìm các giá trị thực của tham số fx=m−3khi x<12m−13khi x=11−7x2+2khi x>1 để hàm số để tồn tại limx→1fx.

Lời giải

Ta có limx→1−fx=limx→1−m−3=m−3limx→1+fx=limx→1+1−7x2+2=−2

Để hàm số có giới hạn tại x = 1 thì limx→1−fx=limx→1+fx.

⇒m−3=−2⇔m=1

Vậy m = 1.

3. Bài tập tự luyện

Câu 1. Tính limx→1−−3x−1x−1 bằng:

A. -1

B. -∞

C. +∞

D. -3

Câu 2. Tính limx→+∞2x2−13−x2 bằng:

A. -2

B. 13

C. 23

D. 2

Câu 3. Tính limx→2x3−8x2−4 bằng:

A. 3

B. 1

C. 4

D. 2

Câu 4. Tính limx→−4x2+3x−4x2+4x bằng:

A. -1

B. 54

C. 1

D. -54

Câu 5. Tính limx→1x3−1x−1 bằng:

A. 13

B. 1

C. 12

D. 2

Câu 6. Tính limx→0x3+1−1x2+x bằng:

A. 4

B. 3

C. 0

D. 1

Câu 7. Tính limx→−∞4x2−x+1x+1 bằng:

A. -2

B. 1

C. 2

D. -1

Câu 8. Tính limx→+∞x+5−x−7 bằng:

A. -∞

B. +∞

C. 0

D. 4

Câu 9. Tính limx→−∞−2x5+x4−33x2−7 là:

A. 0

B. +∞

C. -2

D. -∞

Câu 10. Tính limx→+∞x2−4x−x

A. -2

B. -∞

C. 0

D. +∞

Câu 11. Cho limx→−∞x2+ax+5+x=5. Giá trị của a là:

A. 6

B. 10

C. -10

D. -6

Câu 12. Kết quả đúng của limx→1x3−1x4−1 bằng:

A. 34

B. 4

C. 43

D. 3

Câu 13. Trong các mệnh đề sau, mệnh đề nào đúng?

A. limx→−∞x4−x1−2x=0

B. limx→−∞x4−x1−2x=+∞

C. limx→−∞x4−x1−2x=1

D. limx→−∞x4−x1−2x=−∞

Câu 14. Cho fx=4−x2      −2≤x≤2x2−4x−2                         x>2. Tính limx→−2+fx.

A. 0

B. 4

C. +∞

D. Không tồn tại

Câu 15. Tìm các giá trị thực của tham số m để hàm số fx=x+m khi  x<0x2+1khi  x≥0 có giới hạn tại x = 0.

A. m = - 1

B. m = 2

C. m = -2

D. m = 1

Bảng đáp án

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

C

A

A

B

A

C

A

C

B

A

C

C

B

A

D

Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:

Hàm số liên tục và cách giải bài tập

Phép tịnh tiến và cách giải các dạng bài tập

Phép đối xứng tâm và cách giải các dạng bài tập

Phép đối xứng trục và cách giải các dạng bài tập

Phép quay và cách giải các dạng bài tập