1. Quy tắc cộng
1.1. Định nghĩa
Là khi một việc gì đó có thể làm theo một trong hai phương án: A hoặc B
Giả sử với phương án A có m cách để thực hiện, trong khi phương án B có n cách thực hiện và không trùng với cách nào với A, suy ra công việc đó sẽ có m + n cách để thực hiện.
1.2. Công thức quy tắc cộng
Ta có công thức:
Với các tập
$A_{1},A_{2},...A_{n}$ rời nhau từ đó suy ra:
$left | A_{1}cup A_{2}cup....cup A_{n} right | =left |A_{1} right | +left | A_{2} right | +....+left | A_{n} right |$

2. Quy tắc nhân
2.1. Định nghĩa
Hai công đoạn A và B trong một công việc. Tại công đoạn A có m cách thực hiện, và tương ứng tại công đoạn B có n cách thực hiện tương ứng. Ta sẽ suy ra công việc đó có m . n cách để làm.
2.2. Công thức quy tắc nhân
Ta có các tập $A_{1},A_{2},,...A_{n}$ đôi một và rời nhau
Từ đó ta có:
$left | A1 cap A_{2} cap...cap A_{n} right |=left | A_{1} right |.left | A_{2} right |...left | A_{n} right |$
Đăng ký nhận ngay bí kíp nắm trọn kiến thức và mọi dạng bài thuộc chương trình Toán 11

3. Quy tắc bù trừ (nguyên lý bù trừ)
Khi H là hành động được chia nhiều trường hợp thì ta sẽ đếm phần bù của bài toán theo cách sau:
-
Đầu tiên, đếm số phương án thực hiện hành động H (không xét đến yếu tố có thỏa mãn tính chất T hay không), từ đó ta sẽ suy ra được $alpha$ phương án).
-
Sau đó đếm số phương án làm thực hiện hành động H, không thỏa mãn tính chất T, từ đó ta có $beta$ phương án.
Từ đó: ta có yêu cầu bài toán có những phương án sau thỏa mãn: $alpha - beta$.
4. Một số bài tập về quy tắc đếm từ cơ bản đến nâng cao
4.1. Bài tập tự luận quy tắc đếm kèm phương pháp giải
Bài tập 1 quy tắc đếm lớp 11
Trong kì thi THPT QG 2021, trường Hoài Đức có kết quả tốt nên được chọn một học sinh đi dự trại hè quốc tế. Trường Hoài Đức quyết định chọn một học sinh đạt từ 28,5 điểm trở lên từ các lớp 12A1,12A2 hoặc 12A3. Nhà trường có thể chọn theo bao nhiêu cách khi lớp 12A1 có 5 học sinh đạt trên 28.5 điểm, lớp 12A2 có 4 học sinh và lớp 12A3 có 3 học sinh đạt từ trên 28.5 điểm.
Bài giải:
Chúng ta có thể chọn học sinh thỏa mãn yêu cầu đề bài theo các cách sau
-
Với học sinh lớp 12A1: có 5 cách.
-
Với học sinh lớp 12A2: có 4 cách.
-
Với học sinh lớp 12A3: có 3 cách.
Từ đó theo quy tắc cộng ta có số cách chọn là: 5 + 4 + 3 = 12 cách chọn,
Bài tập 2 quy tắc đếm lớp 11
Có 8 bông hoa tulip khác nhau và 6 hoa ly khác nhau. Tổng cộng có bao nhiêu cách chọn 1 bông hoa?
Bài giải:
Các cách để chọn được 1 bông hoa là
-
Với hoa tulip: có 8 cách chọn,
-
Với hoa ly: có 6 cách chọn.
Áp dụng quy tắc cộng, có tất cả 8 + 6 = 14 cách chọn.
Bài tập 3 quy tắc đếm lớp 11
Ở tủ sách có 12 quyển sách mẫu Văn 12 và 6 quyển mẫu Tiếng Anh 12. Có bao nhiêu cách có thể chọn được 1 quyển sách?
Bài giảng
Có số cách chọn 1 quyển sách là
-
Với sách Văn: có 12 cách
-
Với sách tiếng Anh: có 6 cách
Áp dụng quy tắc cộng, học sinh có 12 + 6 = 18 để chọn một cuốn sách.
Bài tập 4 quy tắc đếm lớp 11
Một em bé có thể mang họ cha là Lê, hoặc họ mẹ là Trần; tên đệm có thể là Hoàng, Đức hoặc Thanh; tên có thể là Tùng, Minh, Đăng hoặc Hùng. Vậy để đặt tên cần phải trải qua bao nhiêu bước.
Bài giải:
Số bước cần để đặt tên là
-
Bước thứ nhất, tìm họ: có 2 cách.
-
Bước thứ hai, tìm tên đệm: có 3 cách.
-
Bước thứ ba, tìm tên: có 4 cách.
Áp dụng quy tắc nhân, có số cách là: 2 . 3 . 4 = 24 cách đặt tên
Bài tập 5 quy tắc đếm lớp 11
Lớp học tại trường Hoài Đức có 40 học sinh. Cô giáo muốn chọn một ban điều hành lớp gồm một lớp trưởng, một lớp phó và một thủ quỹ. Số cách chọn để có mỗi học sinh là một nhiệm vụ là?
Bài giải:
Số bước cần để tìm được ban điều hành là
-
Bước thứ nhất, tìm lớp trưởng: có 40 cách (vì ai cũng có thể lớp trưởng)
-
Bước thứ hai, tìm lớp phó: có 39 cách (vì có một học sinh đã được làm lớp trưởng, nên chỉ còn 39 học sinh có thể làm lớp phó)
-
Bước thứ ba, chọn thủ quỹ: còn lại 38 học sinh nên có 38 cách chọn
Áp dụng quy tắc nhân, ta có 40 . 39 . 39 cách chọn
4.2. Bài tập trắc nghiệm quy tắc đếm có đáp án
Bài 1:
Trong lớp có 20 học sinh nữ và 25 học sinh nam. Cô giáo muốn tìm:
a) Một học sinh đi tham gia trại hè quốc tế
b) Một học sinh nam cùng một học sinh nữ tham gia trại hè quốc tế
Số cách chọn trong mỗi trường hợp a) và b) lần lượt là:
A. 500 và 45 B. 45 và 500 C. 500 và 25 D. 25 và 500.
=> CHỌN ĐÁP ÁN A
a. Ta thấy có hai phương án
Đếm số cách chọn ta có:
-
25 cách chọn cho học sinh nam đi dự trại hè quốc tế
-
20 cách chọn để học sinh nữ đi trại hè
Với quy tắc cộng có 20 + 25 = 45 cách
b. Ta sẽ có hai cộng đoạn chọn học sinh nam và chọn học sinh nữ
Có số cách chọn công đoạn là:
-
Chọn 1 học trong số học sinh nam có 25 cách chọn.
-
Chọn 1 học trong số sinh nữ thì có 20 cách chọn.
Áp dụng quy tắc nhân có 25 . 20 = 500 cách.
Bài tập 2:
Giá sách có 10 quyển sách Toán khác nhau, 8 quyển sách Anh khác nhau và 6 quyển sách Lý khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn nhau?
A. 80. B. 60. C. 48. D. 188.
=> CHỌN ĐÁP ÁN D
Ta có
10 . 8 = 80 cách chọn một quyển sách Toán và một quyển sách Anh khác nhau.
10 . 6 = 60 cách chọn một quyển sách Anh và một quyển sách Lý khác nhau.
8 . 6 = 48 cách chọn một quyển sách Anh và một quyển sách Lý khác nhau.
Áp dụng quy tắc cộng ta có số cách chọn 2 quyển sách khác môn là 80 + 60 + 48 = 188 cách.
Bài tập 3
Một hàng có 3 nam 3 nữ ngồi chung. Có mấy cách xếp để:
a) Cho nữ và nam xe kẽ nhau
A. 72 B. 74 C. 76 D. 78
b) Nữ và nam xen kẽ có một người A là nam, một B nữ cạnh nhau
A. 40 B. 42 C. 46 D. 70
c) Nữ và nam cạnh nhau có C nam, D nữ không cạnh nhau
A. 32 B. 30 C. 35 D. 70
a) Vị trí thứ nhất có 6 cách chọn tùy ý. Sau đó, vị trí ngồi vào thứ 2 có 3 cách chọn. Vị trí thứ ba có 2 cách chọn, vị trí thứ 4 có hai cách chọn, vị trí thứ 5 có 1 cách chọn, vị trí thứ 6 có một cách chọn.
Suy ra sẽ có 6 . 3 . 2 . 2 . 1 . 1 = 72 cách.
=> CHỌN ĐÁP ÁN A
b) A, B nam nữ ngồi vào chỗ thứ nhất và thứ 2 là hai cách. Sau đó, hai cách chọn ở chỗ thứ ba, 2 cách chọn ở chỗ thứ tư, 1 cách chọn chỗ thứ năm, 1 cách chọn chỗ thứ sáu.
Cuối cùng, A, B nam nữ ngồi vào hai chỗ hai và ba. Lúc đó, có 2 cách chọn ở chỗ thứ nhất, 2 cách chọn ở chỗ thứ tư, 1 cách chọn ở chỗ thứ năm, 1 cách chọn ở chỗ thứ 6.
Với khi A, B nam nữ ngồi tại chỗ thứ 3, 4; 4, 5; 5, 6.
Tại đó có: 5 . 2 . 2 . 2 . 1 . 1 = 40 cách.
=> CHỌN ĐÁP ÁN A
c) Để nam nữ không ngồi kề nhau, ta có số cách chọn là
Từ đó ta có: 72 - 40 = 32 cách
=> CHỌN ĐÁP ÁN A
Bài tập 4
Cho các chữ số1, 2, 3, 4, 5, 6, 7, 8, 9, số tự nhiên gồm năm chữ số đôi một khác nhau lớn hơn 50000 có bao nhiêu số?
A. 8400 B. 15120 C. 6720 D. 3843
=> CHỌN ĐÁP ÁN A
A,b,c,d là các số đôi một khác nhau thì số cần tìm là abcde
$a epsilon left { 5,6,7,8,9 right }$
Từ đó có thể nhận ra: 5 cách chọn với a, 8 cách chọn với b, 7 cách chọn với c, 6 cách chọn với d, 5 cách chọn với e.
Suy ra có tất cả là 5 . 8 . 7 . 6 . 5 = 8400 (số).
Bài tập 5
Lập được bao nhiêu số có bốn chữ số khác nhau, luôn xuất hiện chữ số 4, chia hết cho 20 từ các chữ số 0, 2, 3, 4, 5, 7, 8 ?
A. 36 B. 24 C. 32 D. 40
=> CHỌN ĐÁP ÁN A
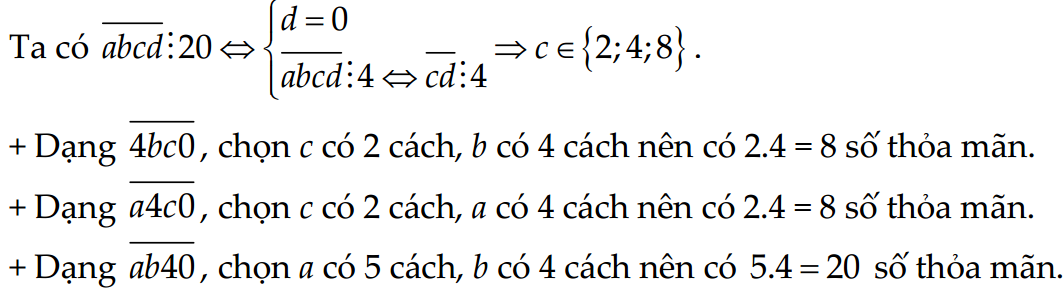
Vậy có 8 + 8 + 20 = 36 số
Bài tập 6
Lập được bao nhiêu số chia hết cho 25, có bốn chữ số khác nhau, từ các chữ số 0, 2, 3, 4, 5, 6, 7?
A. 36 B. 60 C. 52 D. 38
Lời giải:
=> CHỌN ĐÁP ÁN C

Suy ra có 20 + 16 + 16 = 52 số.
Bài tập 7
Lập được bao nhiêu số chia hết cho 20 có bốn chữ số khác nhau từ các chữ số 0, 1, 2, 3, 4, 6, 7
A. 60 B. 52 C. 46 D. 64
Lời giải:
=> CHỌN ĐÁP ÁN A
Ta có $overline{abcd}, vdots , 20 , begin{matrix} Leftrightarrow left{begin{matrix} d=0 overline{abcd} , vdots , 4 Leftrightarrow overline{cd} , vdots , 4 end{matrix}right. & Rightarrow & c , epsilon left { 2;4;6 right } end{matrix}$
Ta thấy có 3 cách chọn c, có 5 cách chọn a, có 4 cách chọn b
Suy ra có 3 . 5 . 4 = 60 số.
Bài tập 8
Có 5 quyển sách Toán, 6 quyển sách Lý và 8 quyển sách Hóa. Các quyển sách này không giống nhau
a) Chọn 1 quyển sách có số cách là
A. 19
B. 240
C. 6
D. 8
b) 3 quyển sách khác môn nhau là
A. 19
B. 240
C. 969
D. 5814
c) 2 quyển sách khác môn nhau là
A. 38
B. 171
C. 118
D. 342
Bài giải:
a. Có số cách là 5 + 6 + 8 = 19
=> CHỌN ĐÁP ÁN A
b. Có số cách là 5 . 6 . 8 = 240
=> CHỌN ĐÁP ÁN B
c. Có số cách là 5 . 6 + 5 . 8 + 6 . 8 = 118.
=> CHỌN ĐÁP ÁN C
Bài tập 9
Số chẵn có hai số có số lượng số là
A. 14
B. 45
C. 15
D. 50
Số cần tìm có dạng: $overline{ab}$ ($a neq 0$; b chẵn)
a có 9 cách chọn (1 -> 9) và b có 5 cách chọn ( 0, 2, 4, 6, 8).
Suy ra có 9 . 5 = 45 số.
=> CHỌN ĐÁP ÁN B
Bài tập 10:
Hai chữ số khác nhau có bao nhiêu số lẻ
A. 40
B. 13
C. 14
D. 45
Số cần tìm có dạng $overline{ab} (a neq 0, a neq b, b$ lẻ)
B có 5 cách chọn là 1, 3, 5, 7, 9, ứng với mỗi cách chọn có 8 cách chọn b (trừ 0 và b).
Suy ra có 5 . 8 = 40 số.
=> CHỌN ĐÁP ÁN A
Đăng ký ngay để được các thầy cô tổng hợp kiến thức và xây dựng lộ trình ôn thi tốt nghiệp THPT sớm từ bây giờ

Trên đây là toàn bộ lý thuyết và cách giải bài tập quy tắc đếm thường gặp trong chương trình Toán 11. Tuy nhiên nếu em muốn đạt kết quả tốt thì hãy làm thêm nhiều dạng bài khác nữa. Các em học sinh hãy tham khảo Vuihoc.vn và đăng ký tài khoản để luyện đề!
Bài viết tham khảo thêm:
Hàm số lượng giác
Phương trình lượng giác thường gặp
Hoán vị, tổ hợp, chỉnh hợp


